Původní verze: 29.3.-23.4.2013, aktualizováno 6.-7.11.2023.
Před nějakou dobou proběhly tiskem články o tom, že není známá rovnice popisující tvar vejce (např. ihned.cz, novinky.cz, iprima.cz). Nikdy před tím jsem nad tvarem vejce z matematického hlediska nepřemýšlel, až do přečtení těchto článků. Napadlo mě následující řešení: Každá ze špiček vajíčka, tedy tupá i ostrá připomíná rotační elipsoid. Je tedy možné, že jde o dva elipsoidy, které plynule přecházejí jeden do druhého. Zkusil jsem tedy takovouto křivku naprogramovat pomocí SW Scilab. Výsledek předčil očekávání. Zdá se, že tímto vznikne univerzální parametrická rovnice vejce, která je schopná zobrazit různé tvary vajec od kulových až po protáhle elipsovité. Navíc je možné tuto rovnici dále rozvíjet.
Odvození rovnice:
Vyjdeme z rovnice elipsy (1) (podle wikipedia.org):
\bigg(\frac x a\bigg)^2+\bigg( \frac y b\bigg)^2=1 \kern14em (1)
Rovnici (1) upravíme do tvaru (2):
y=\pm b\cdot\sqrt{1- \bigg(\frac x a\bigg)^2}\kern1em \LARGE ; \normalsize \kern1em\forall x \in\langle-a;a\rangle \kern7em (2)
Dále předpokládáme, že obě elipsy mají stejnou poloosu a, tedy a1=a2=a, ale obecně různé poloosy b, tedy b1≠b2. Váha parametru b1 se mění od 1 v bodě x=-a do 0 v bodě x=a, a opačně váha parametru b2 je v bodě x=-a 0 a postupně roste na 1 v bodě x=a. Do rovnice (2) tedy za parametr poloosy b dosadíme vážený průměr hodnot b1 a b2, viz rovnice (3):
b=b_1\cdot\frac {(x-a)} {-2\cdot a} + b_2\cdot\frac {(a+x)} {2\cdot a}=\frac {b_1\cdot(a-x)+b_2\cdot(a+x)} {2\cdot a} \kern2em (3)
Celkovou rovnici obvodové křivky vajíčka (4) získáme dosazením rovnice (3) do rovnice (2):
y=\pm \frac {b_1\cdot(a-x)+b_2\cdot(a+x)} {2\cdot a} \cdot\sqrt{1- \bigg(\frac x a\bigg)^2}\kern1em \LARGE ; \normalsize \kern1em\forall x \in\langle-a;a\rangle \kern2em (4)
Výsledné zobrazení:
Na Obr. 1 je porovnání kružnice (černě) o poloměru a (to je z důvodu možného zkreslení obrázku při zobrazení na monitoru či při tisku), modrá je elipsa 1, zelená elipsa 2 a výsledné vajíčko je červeně. Na Obr. 2 a Obr. 3 jsou pak zobrazeny čisté křivky vajíček pro různé hodnoty parametrů b1 a b2.
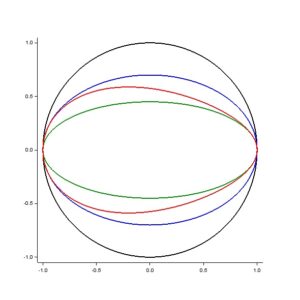
Obr. 1: porovnání původních elips a křivky vajíčka (červeně), kde a=1 (černá kružnice), b1=0.7 (modrá elipsa) a b2=0.4 (zelená elipsa).
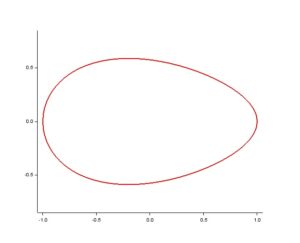
Obr. 2: křivka vajíčka, pro a=1, b1=0.7 a b2=0.4.
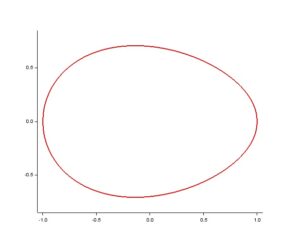
Obr. 3: křivka vajíčka, pro a=1, b1=0.8 a b2=0.6.
Závěr
Závěrem lze říci, že rovnice (4) dobře popisuje tvary různých vajec, které jsou určeny pomocí parametrů a, b1 a b2. Rovnici určující parametr b (3), lze zřejmě podle potřeby zvolit i jinak, ale výsledné křivky se zdají být dobré i podle tohoto tvaru.
Poznámka:
Původní umístění této stránky ja na serveru geoterra.eu. Tenkrát, když jsem ty rovnice sestavoval, udělal jsem v úpravě rovnice pro elipsu chybu, která se promítla i do celkové rovnice vajíčka. Tato chyba se ovšem neprojevila, a to z důvodu použitého parametru a=1. Pro jakoukoli jinou hodnotu tohoto parametru by se to bývalo projevilo a já bych na to přišel hned. Takto jsem si toho všimnul až po více než 10ti letech 🙂
